【向量数据库】向量存储内存_热门推荐_行情

【向量数据库】向量存储内存

2025-01-29 16:50 浏览:72

对于海量的向量数据，除了搜索速度以外，内存的开销也是一个巨大的挑战。

举个例子，假如向量的维度是128，每个维度的数值是一个32位的浮点型数，那么一个向量占用内存的大小就是：512字节
在这里插入图片描述
如果库中一共有1千万个向量，那么总共占用的内存：大约4.77GB

实际上在真实应用场景中，上千的向量维度和上亿的向量数量都不并稀奇，因此内存开销的问题大约的确是严重的。每个向量都对应着一个切实有用的记录，所以不太可能通过纵向的删除某些向量来节省内存，那唯一的选择只能是想办法横向的把每个向量本身的大小给降下来。

乘积量化 - Product Quantization

质心向量

有一种方法是这样的，已经介绍过k-means聚类算法，这些相邻的有一定聚集的向量最终被分为了一类，它们有一个聚类中心，一般也叫质心。
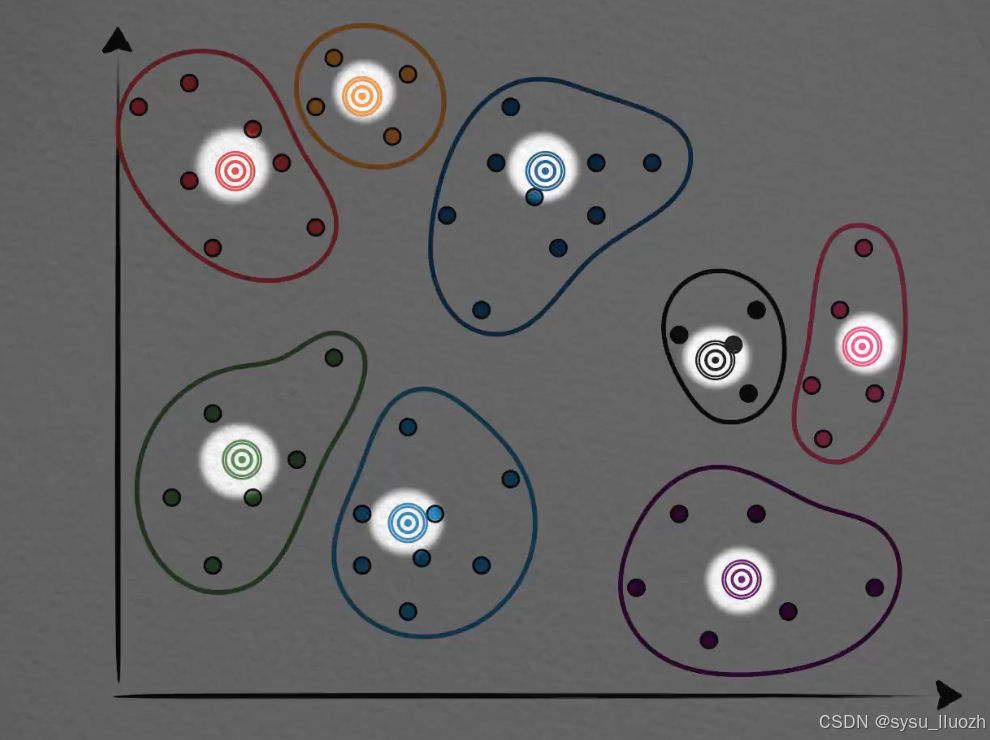
在这里插入图片描述
那么，能不能直接用质心向量来表示，或者说替代这个聚类中所有的向量呢？比如在这个分类中，[0.2, 0.8]这个向量用它所在的分类质心向量[0.23, 0.88]来表示，同样这个[0.43, 0.82]也用质心向量[0.23, 0.88]来表示。
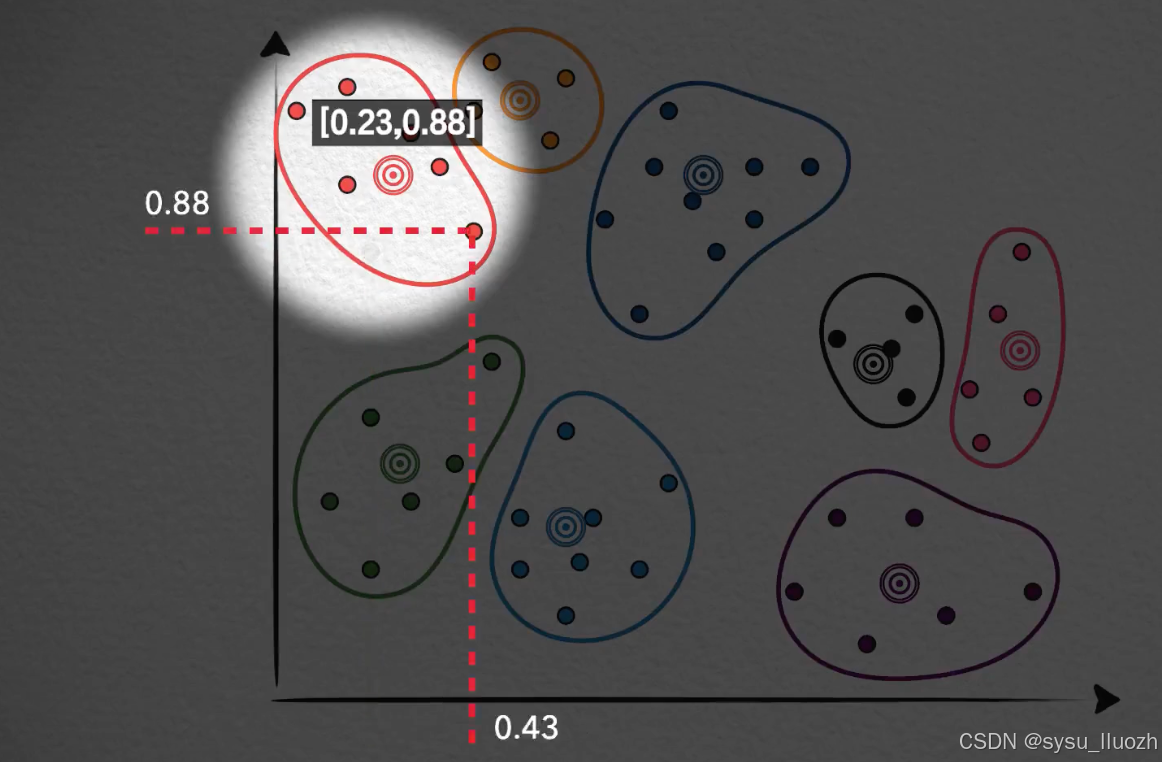
在这里插入图片描述
这个分类中的每个向量都用质心向量来替代表示，每个分类中的每个向量点都如此这般。大约是可以的，这实际上就是一种典型的有损压缩的方法。

用一张图片来举个例子，图片是由像素点组成的，而一张彩色照片上的每一个像素点都有RGB三个数值，所以可以把一个像素点看作是三维空间中的向量点
在这里插入图片描述
所以这张图片在像素空间中其实是这个样子的

接下来用一个只有少量点的图来代替说明上面的像素空间，在这些点上用聚类算法得到一些分类，然后让图片中所有的像素点都被所在分类的质心点所替代，比如下面这个像素点，在像素空间的这个位置，被聚到了这个类中，质心点在这里，于是用它所在分类的质心点来替代这个具体的像素点。
在这里插入图片描述
图片中的每个像素点都被其所在分类的质心点所替代，图片最后变成了这样

在这里插入图片描述

虽然质量有所下降，但仍然很大程度上保留了原图的样貌。聚类的数量越多，还原度也就越高，反之越低。
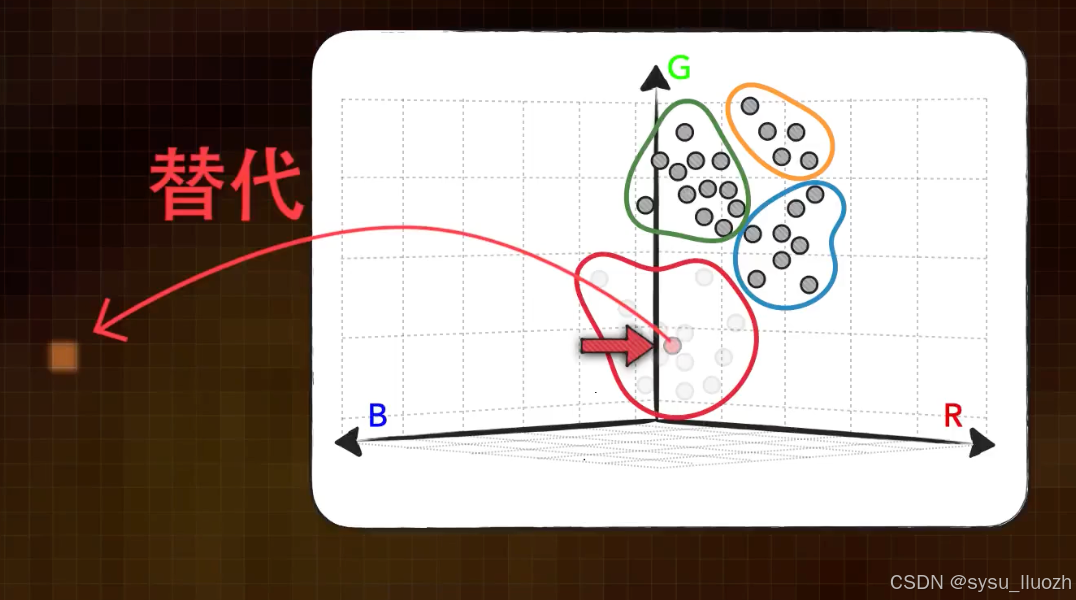
在这里插入图片描述

用质心点来表示具体的向量点，这虽然会丢掉向量的具体值，但考虑到聚类质心和它所在分类中向量点的相关程度，所以仍然很大程度上继续保留着一些原始的信息。而相比于这个有损过程所带来的细节丢失，这样做所带来的好处是非常可观的。

质心编码

如果给这些质心编码，如此用单个的编码值就能存储一个向量，减少了存储空间
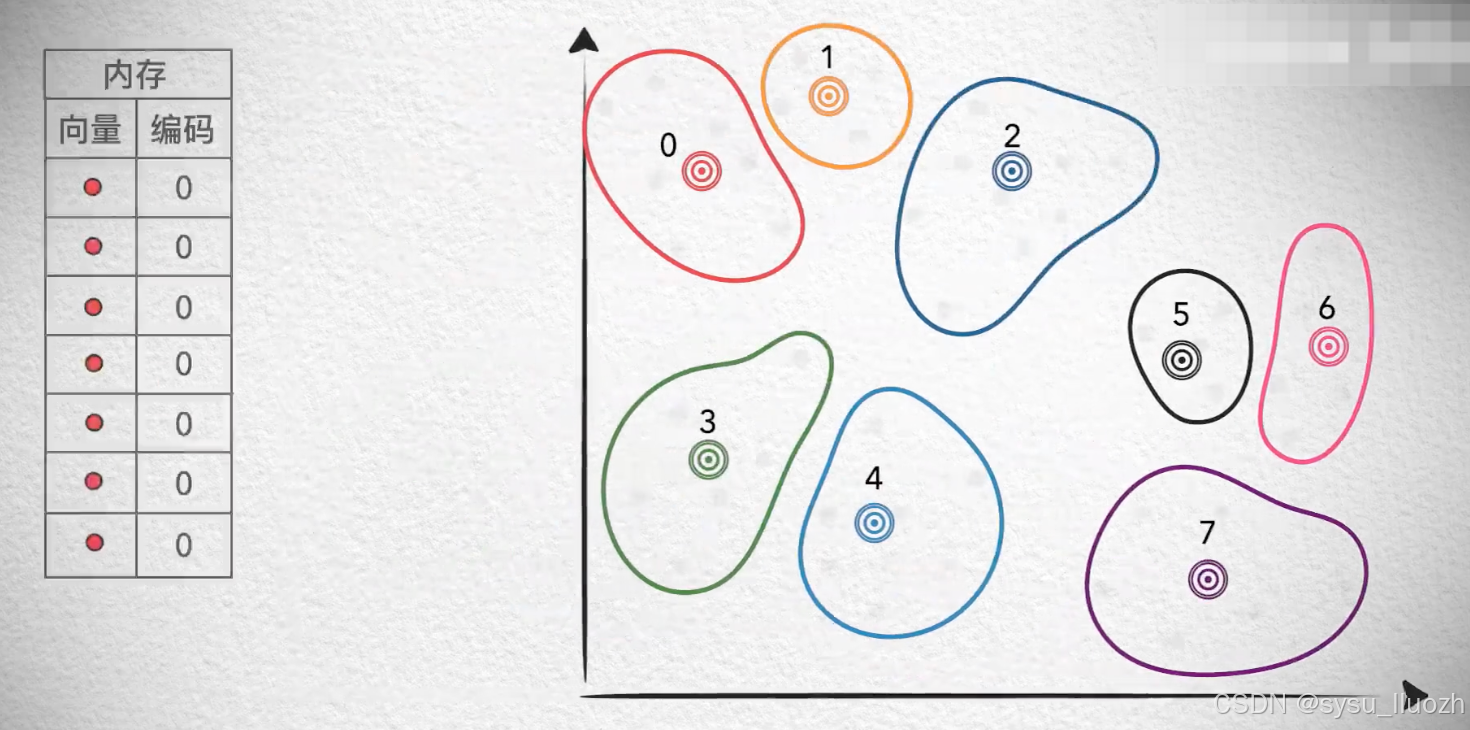
在这里插入图片描述

而把每个质心向量值和它的编码值记录下来，形成一个码本。
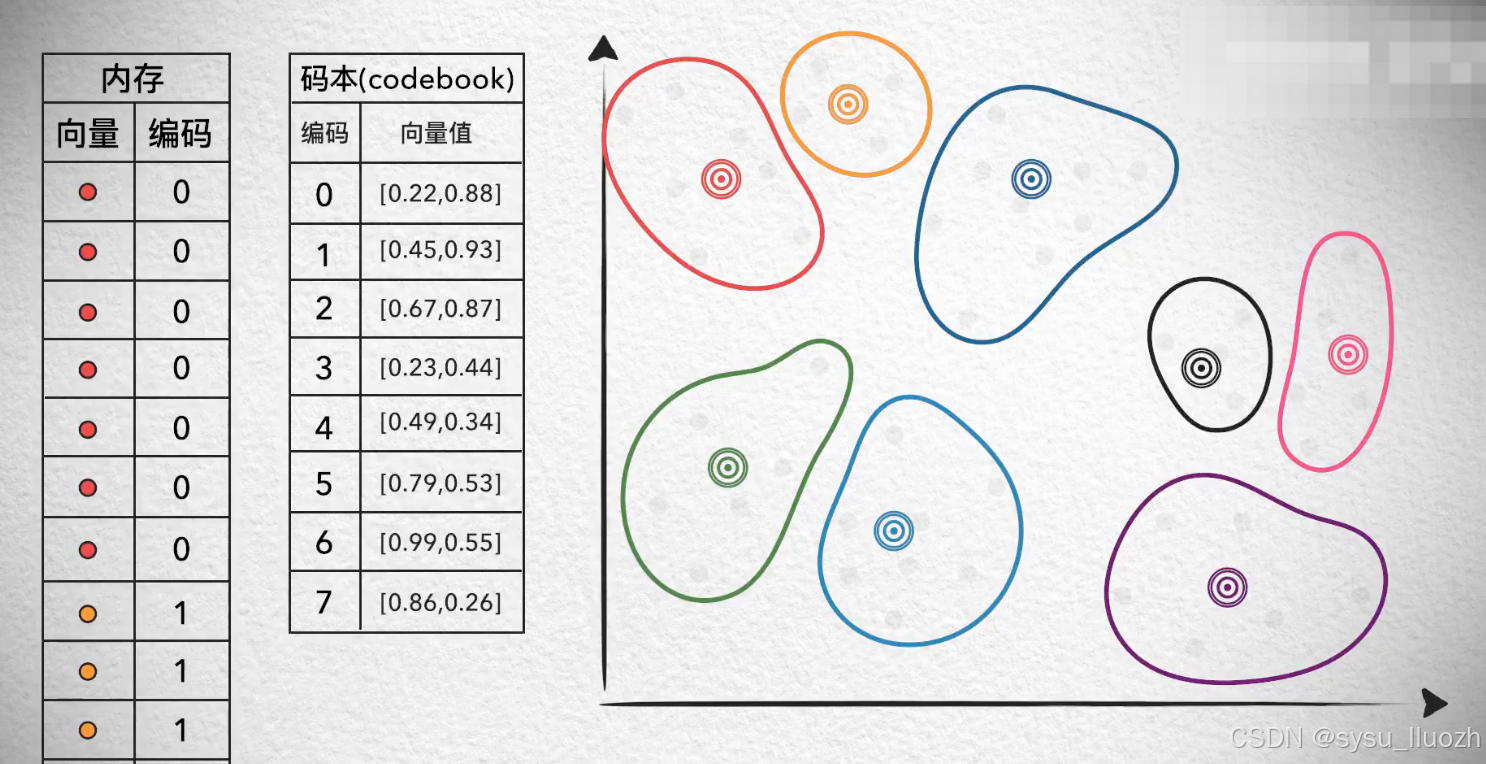
在这里插入图片描述

如此，每次使用某个向量的时候，用它的编码值从码本中找到对应的质心，再复原出质心向量的具体值
在这里插入图片描述
虽然这个向量已经不再是当初的样子，但就像在前面说的那样，问题不大。把向量用质心编码表示，也就是所谓的量化（Quantization）

一个值得注意的问题是，这里虽然把一个二维的向量压缩成了单个编码值，但数据大小却并非降低一半。因为质心的数量是有限的，这里是8个，也就是说这些编码值的取值范围只能说0-7
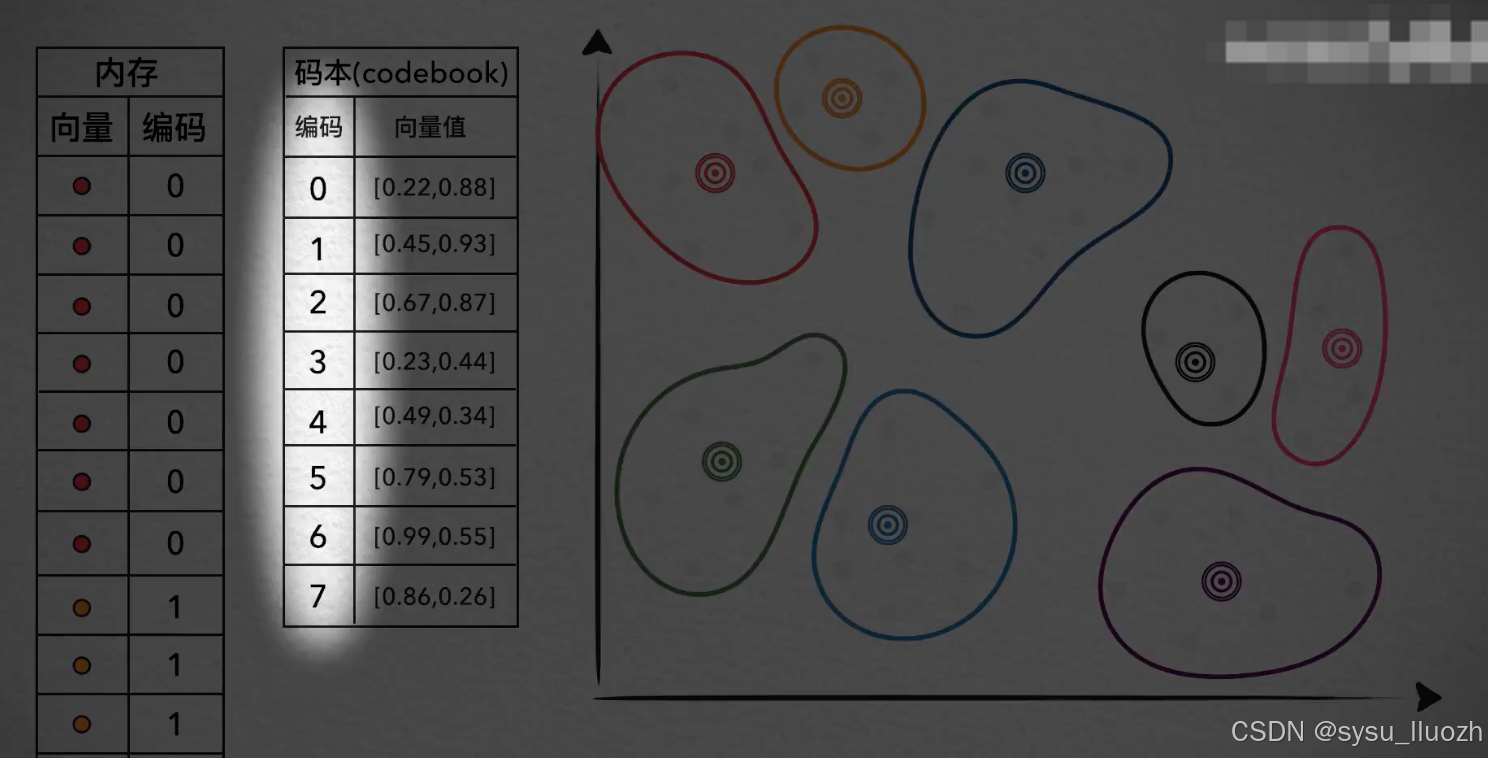
在这里插入图片描述
所以完全可以只用一个字节来存储这些编码值，但对于原始的向量，每个维度数值一般都是浮点型，比如说32位的浮点型数，所以一个原始向量占用的内存其实8字节，所以其实是节省了8倍的内存开销

但对向量进行量化处理之后，却多出了一个额外一个的码本。向量本身的内存开销肯定是降下来了，但难道这个码本就不会产生新的内存开销吗？当然会，而且相当的可观。这在低维的二维向量和三维向量中可能还不太明显，但在真实场景的几百上千维的高维向量数据中，这个码本将变得非常的恐怖。

聚类数量

首先认识一个事情：在数量一定的情况下，要保证量化的质量，分布越稀疏的向量就需要越多的聚类数量。
比如有这么一些向量，如果如此的密集，那大约只需要两个类就就能得到还不错的量化效果
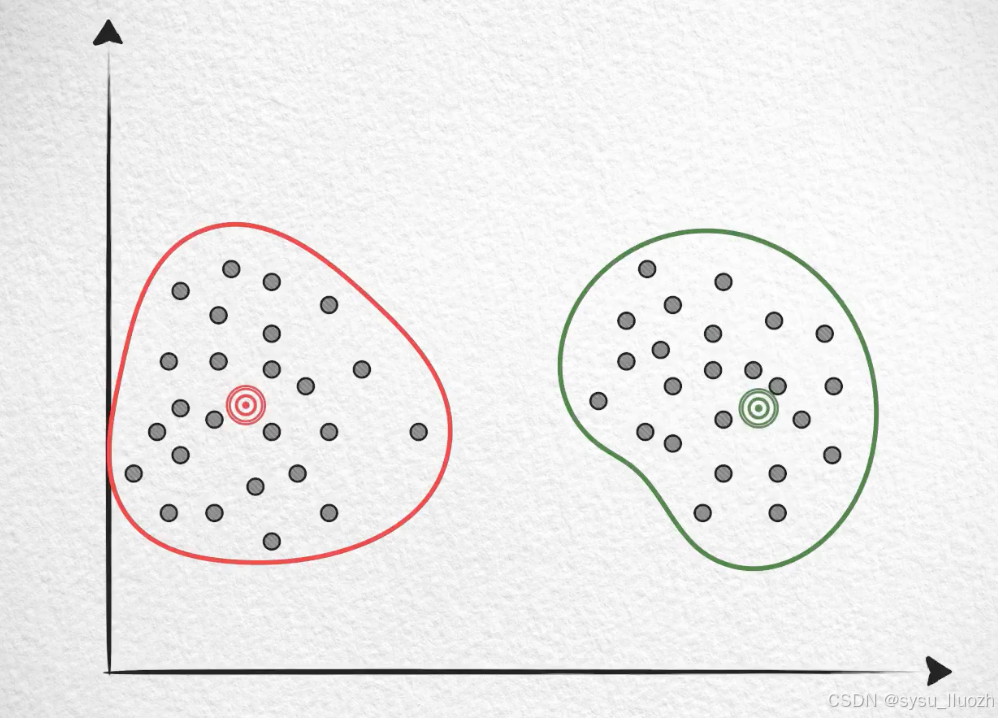
在这里插入图片描述
因为聚类中的每个向量和质心都不太远。但如果稍微稀疏一些，如果还是两个聚类，那质量就不太好了。

因为有很多向量和质心的距离其实很远，所以可能需要聚4类才能保证效果

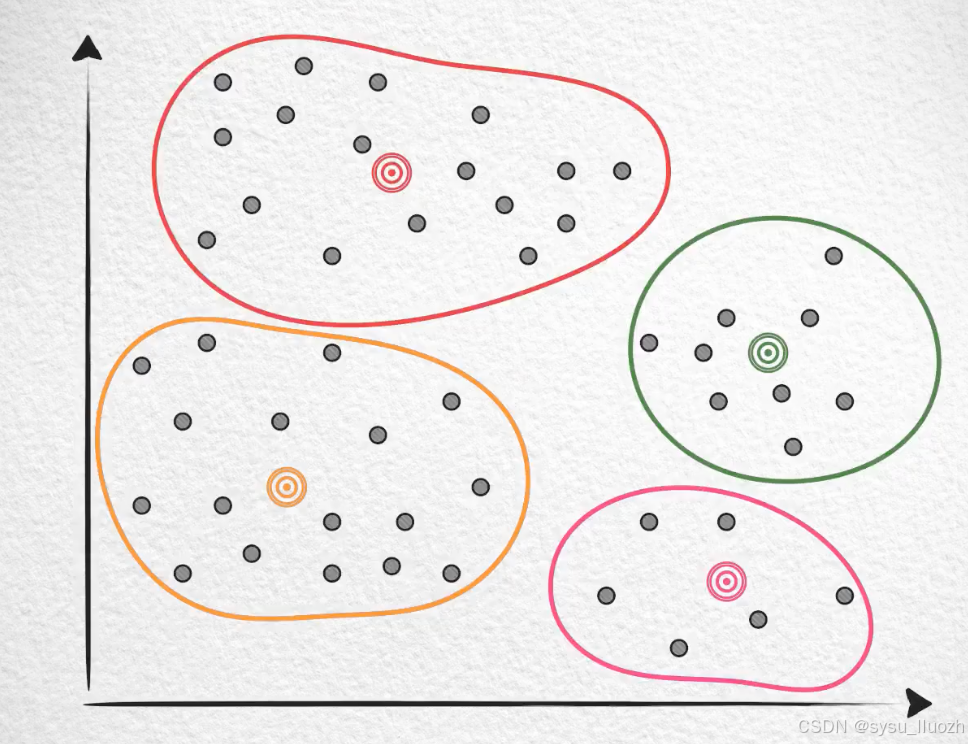
如果是这样的，那可能需要8个，乃至12个聚类才能继续保持。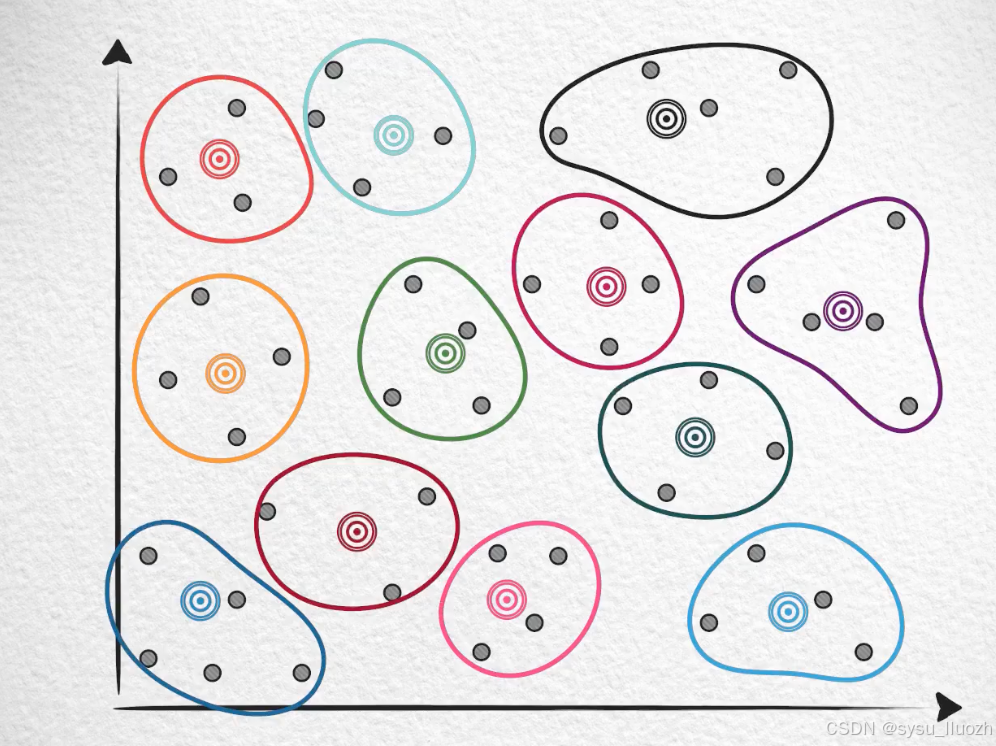在这里插入图片描述

维度灾难

而维度的增加将导致空间爆炸式的扩张，从而迅速的导致向量的分布变得越来越稀疏，比如还有一些随机向量。

在一维空间中的分布可能是这样的
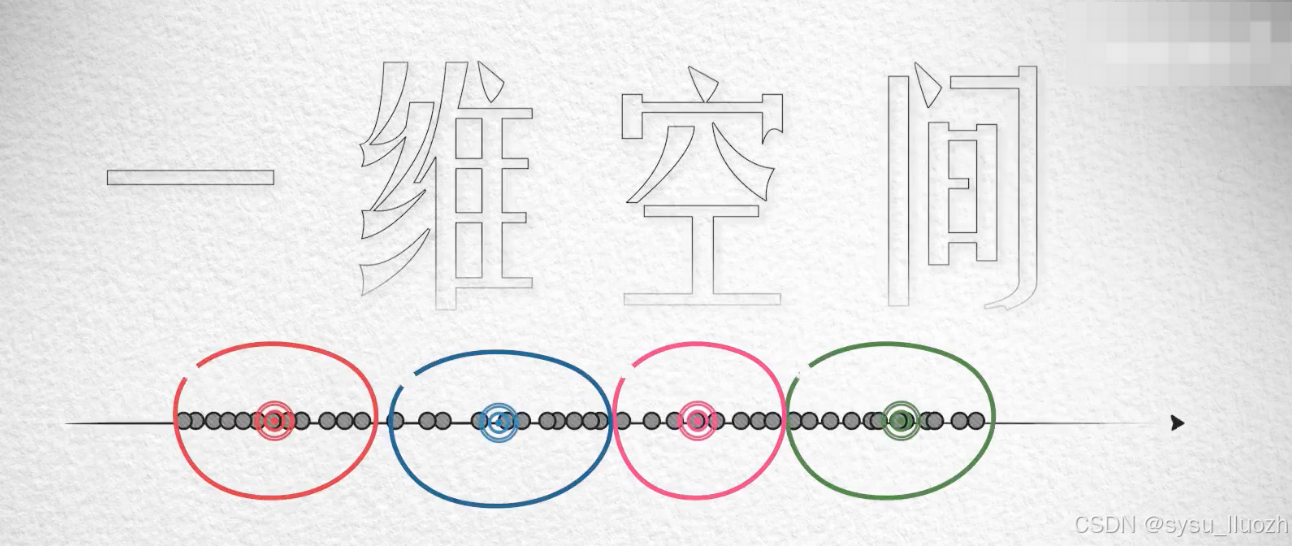
在这里插入图片描述
大约用4个质心就可以完成还不错聚类效果

在二维这个"更广阔"的空间中的分布，可能是这样的，稀疏很多
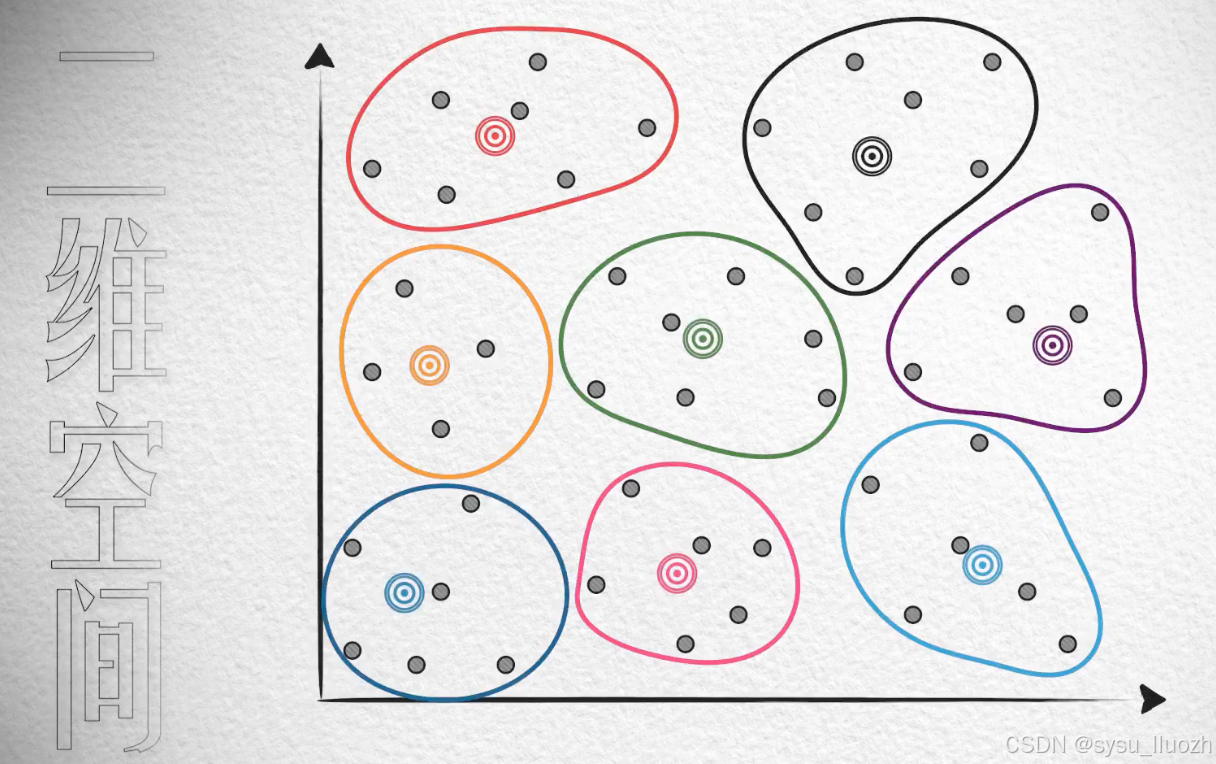
在这里插入图片描述
大约需要8个质心才能保证效果

如果是3维那将更为稀疏
在这里插入图片描述
可能需要几十个质心才能继续保证效果

如此这般，对于实际应用中几百上千维的向量，数据的稀疏令人窒息。因此在如此高维的空间中，为了保证向量在量化后信息仍然得到了很好的保留，得到较高的量化质量，可能需要非常非常大的聚类数量。这也被称之为维度灾难问题。

一个典型的情况是，128维的向量可能需要2^64个聚类中心，这是个大到不可接受的数字。
在这里插入图片描述
因为这将导致用来记录质心编码和向量值的码本变得非常非常的巨大

而为了保存这个巨大的码本所消耗的内存，已经超越乃至远远超越了量化本身所节省下来的内存。

接近这个问题的办法：
在这里插入图片描述

高维的向量分割成若干个低维的子向量
在这些子向量上独立进行量化

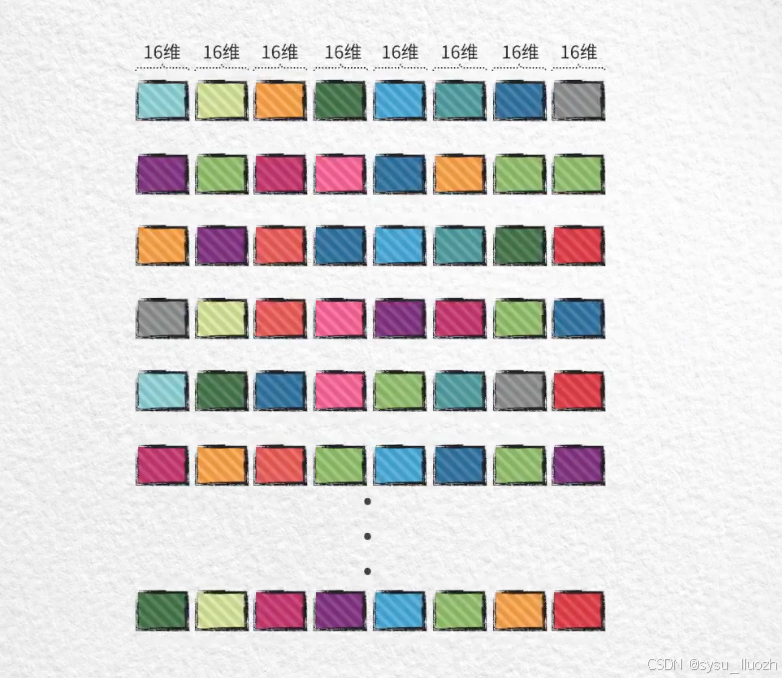
比如把128维的向量分为8个16维的子向量
在8个16维的子空间中分别独立的对子向量进行k-means聚类训练
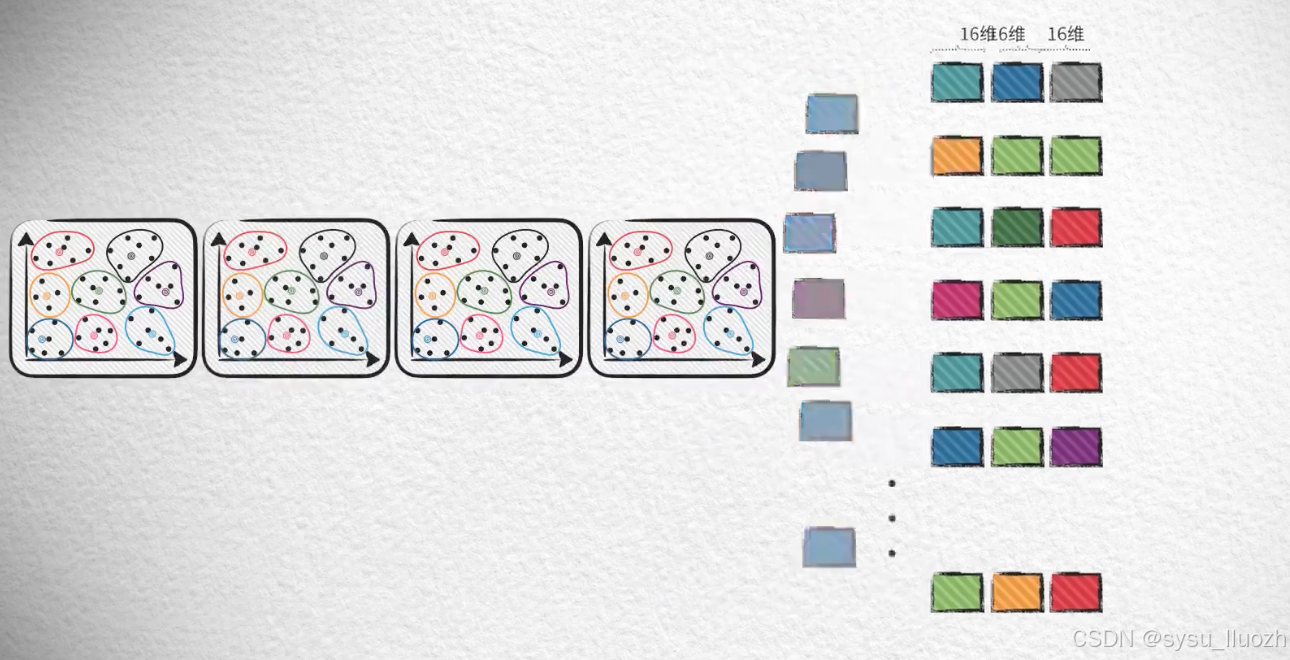
每个向量使用8个子空间的训练结果对自己对应的8个子向量进行量化
每个子向量的维度是16所以每个子空间只需要大约256个聚类数量

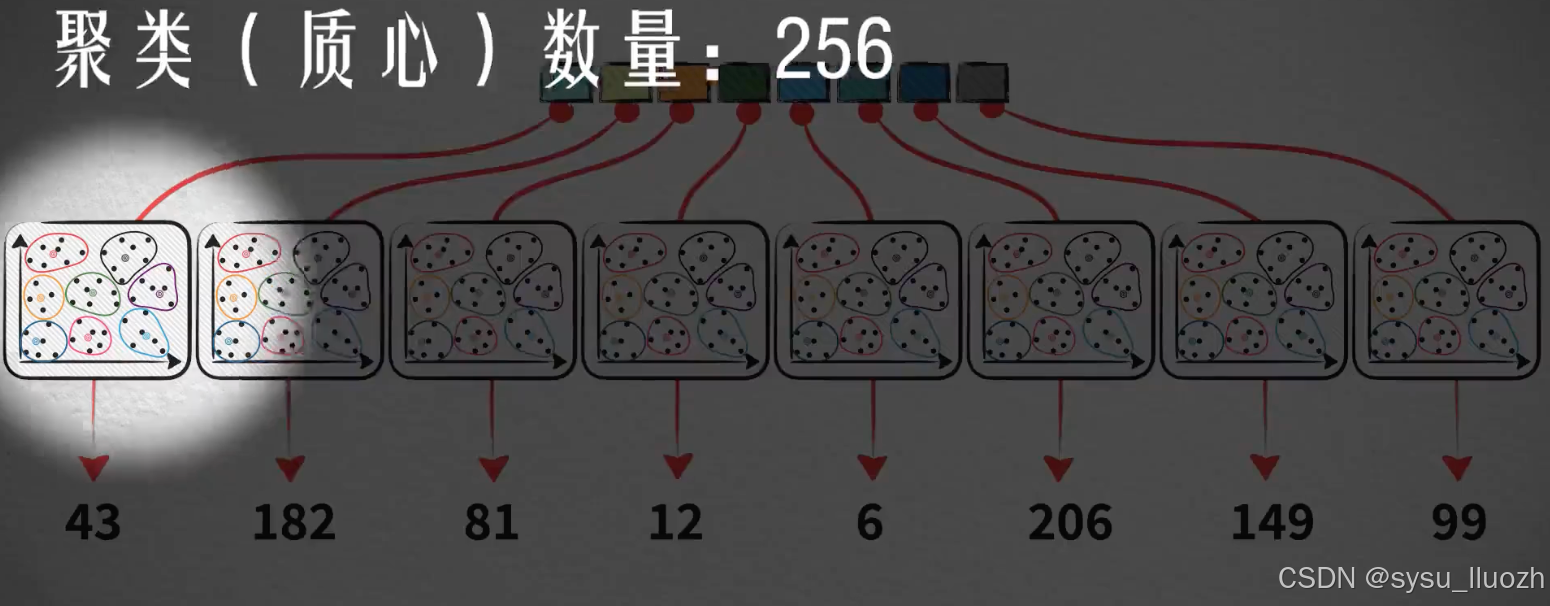
所以每个子向量的量化编码值的范围是0-255
把8个子向量的量化编码值合并在一起得到原始向量最终的量化编码值

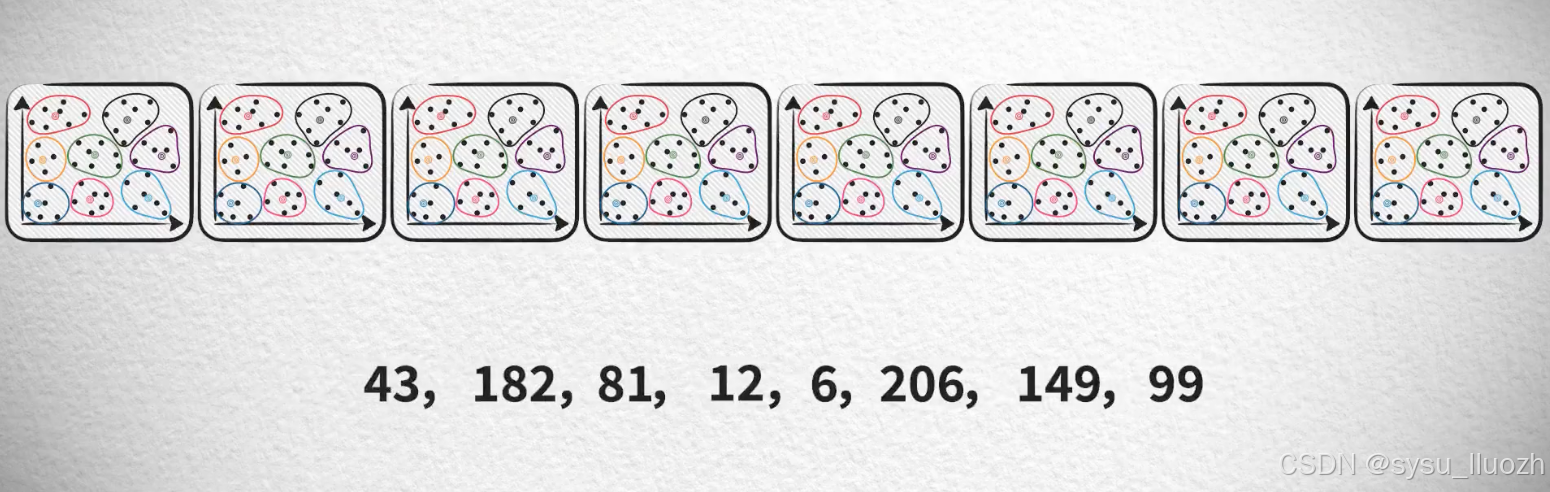
现在一个向量被量化为8个编码值
每个子空间构建自己的子码本
使用的时候用8个编码值分别从对应的子码本中查询出8个16维的子向量
拼接起来复原出一个128维的向量

其实这就是各个子空间量化（Quantization）结果的笛卡尔积（Cartesian product），所以这个算法的名字就叫：（乘）积量化Product Quantization，简称PQ

由于每个子空间的聚类向量只有256，所以每个子码本将变得很小，小到和数据本身相比基本可以忽略不计。
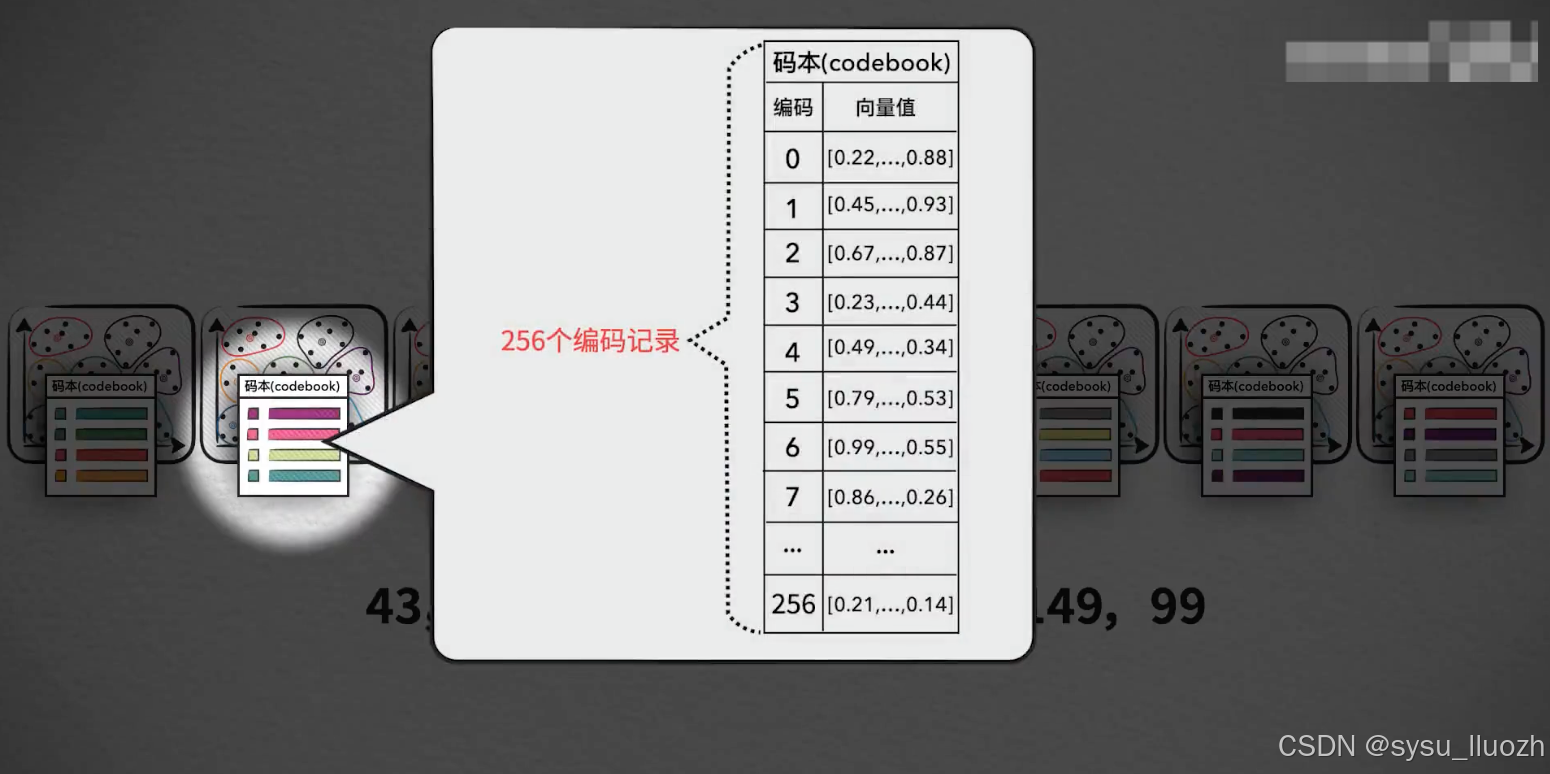
在这里插入图片描述
而8个子空间的"小码本"，放在一起得到的"大码本"也仍然足够的小

仔细思考其中的逻辑，就会发现子空间拆分实际上是把聚类数量，或者说码本大小的增长，从指数模式变成加法模式
在这里插入图片描述

实际上，在解决了维度灾难问题之后，在高维向量数据上能节省的内存是十分惊人的。现在每个128维向量量化后是8个子空间的编码值，而每个编码值的范围在0-256之间，所以只需要1个字节就可以存放的下，8个编码值一共需要8个字节
在这里插入图片描述
因此1千万个向量最终所占的内存总容量是：大约76MB

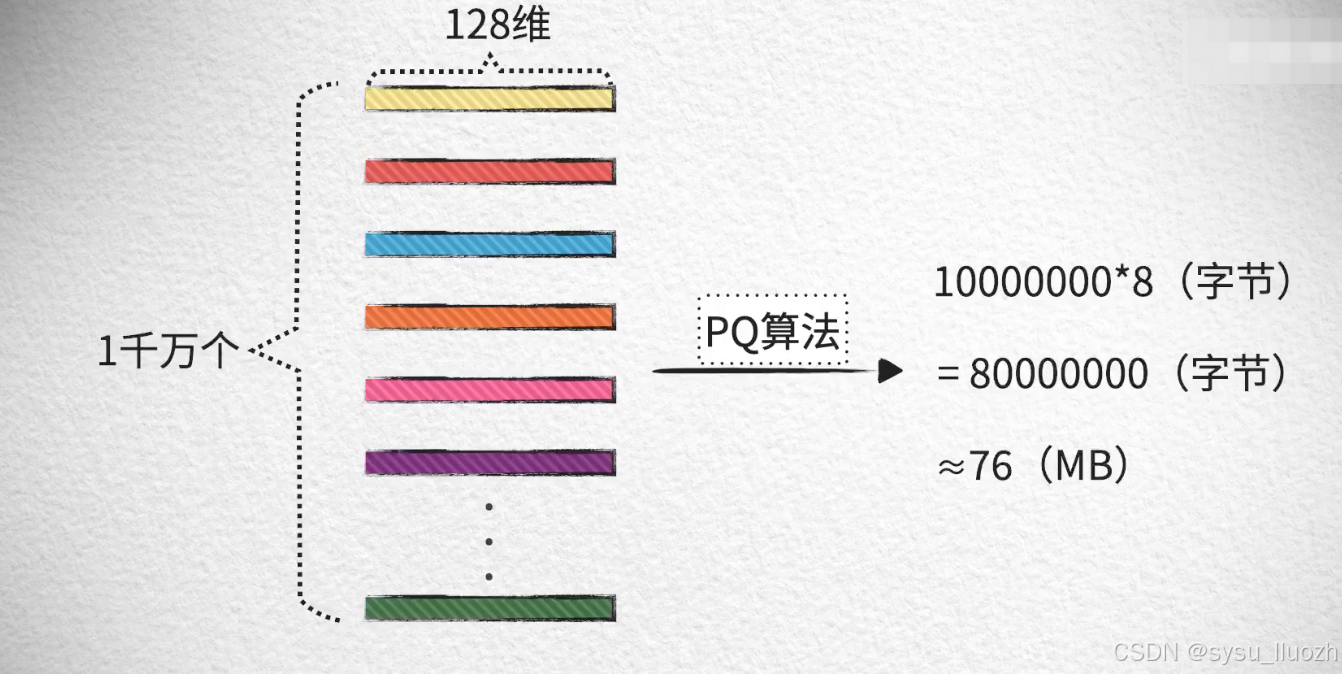
而最开始计算的，没有经过PQ处理的是4.77GB，节省了大约98%的内存开销。

PQ的主要目的虽然是减少内存占用，但是其实也能一定程度的提高搜索速度。可以通过分析复杂度来发现这一点，不过和爆搜相比，虽然快来一点，但从计算复杂度的角度来看仍然是O(n)，属于线性阶。

把提速度和减内存的方法相结合使用，同时实现速度和内存的优化。
速度、质量和内存开销，这三个因素从理论上来说对于一个近似最近邻算法都很重要，但在工程实践上，内存开销似乎就不如另外两个了，因为内存开销仅仅被开发者所感知，但速度和质量却实实在在的被用户所感知。所以如果可以用内存去换质量和速度，也不失为一种实用的算法。

最近老家的房子正在装修，有时候和一些装修师傅聊天，一件有意思的事情是往往聊着聊着就发现我们都认识某个人，遇到6个装修师傅中有3个都是如此，还有一个虽然并不直接认识，但他知道有这么个人的存在。鉴于老家是一个很小的县城，圈子很小，所以其实也并不十分稀奇。但据说即使放眼全国乃至全世界，一个人想要和另外一个人建立联系，只需要通过大约6个人的引荐就能实现，这就是"6人理论"。

如果把人看作是向量点，把搜索看作是让一个人去找另外一个人的过程。比如查询向量在这里，要从这些向量中找出最近似的向量。随机从一个点开始，然后判断这个点的友节点中最为接近查询向量的点。到这个点，再判断它的友节点中最接近的点，如此往复，直到搜索到一个所有友节点都没有自己距离目标近的点，完成搜索。最后这个点就是最相似的。
在这里插入图片描述
一种基于这种想法的算法，有一个很酷的名字叫：导航小世界（NSW）

德劳内三角剖分法 - Delaunay triangulation algorithm

一个棘手的问题是：这些向量点不像人那样拥有社交账号，并通过互相加好友自动形成关系，所以首先要手动给它们建立图结构。当然这种图结构可不是乱建的

比如这样的图结构不靠谱，出现一些无法触达的孤立点
在这里插入图片描述

比如这样的图结构，很多非常近的点没有建立连接，以至于在搜索的时候出现走弯路的问题
在这里插入图片描述

所以在手动构建的图结构的时候，最好保证这些性质：

每个点都有直接连接友节点
如果两个点之间的距离近到一定程度，一定要连接起来形成友节点的关系
在这两个基础上保证连线最少

一种能满足这些性质的方法称之为：德劳内三角剖分法（Delaunay triangulation algorithm）

然而利用德劳内三角剖分法（Delaunay triangulation algorithm）构建的图结构在搜索的时候也不一定能够很快，比如库中的向量数据很多，而查询向量和随机入口却在距离很远的两端，便需要经过很长的一段路才能达到。

把这些向量点拿出来
随机的一个个的放回向量空间
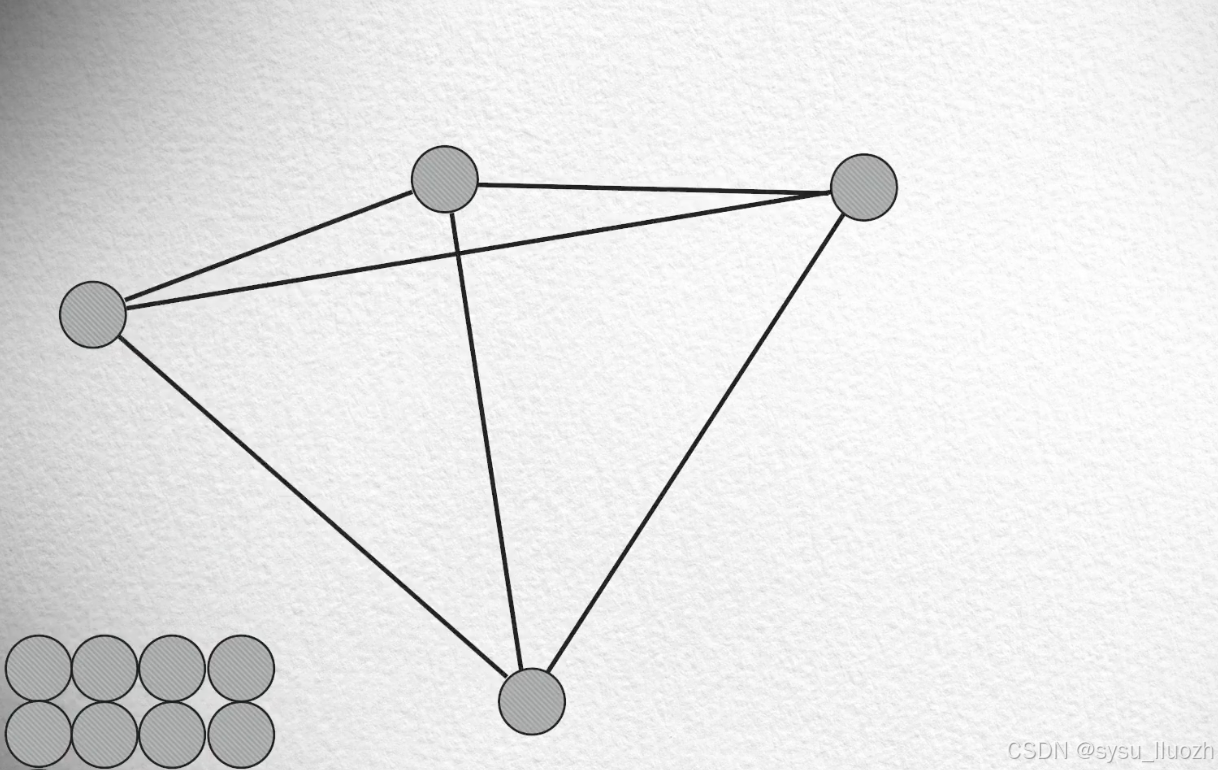
在每次放回一个点的时候，找到最近的几个点建立连接（比如3个点）
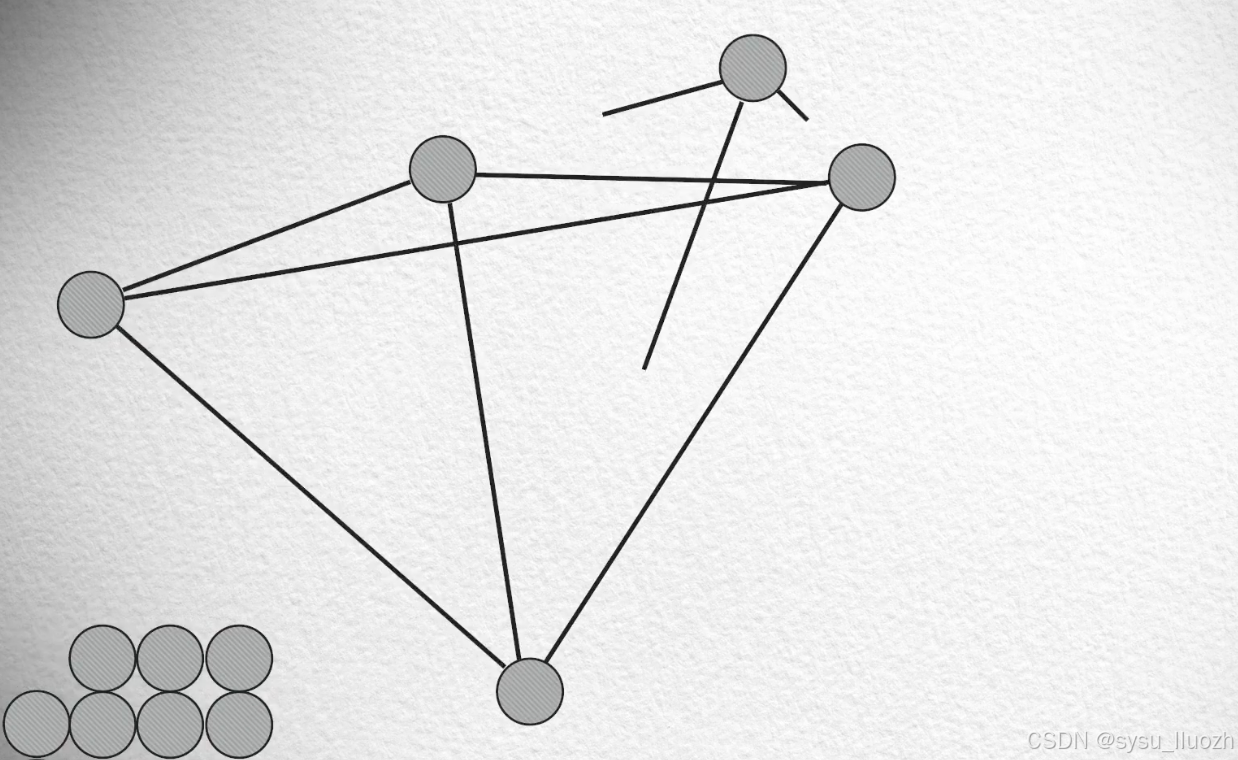
如此把所有的点都放回去后，这个图就建好

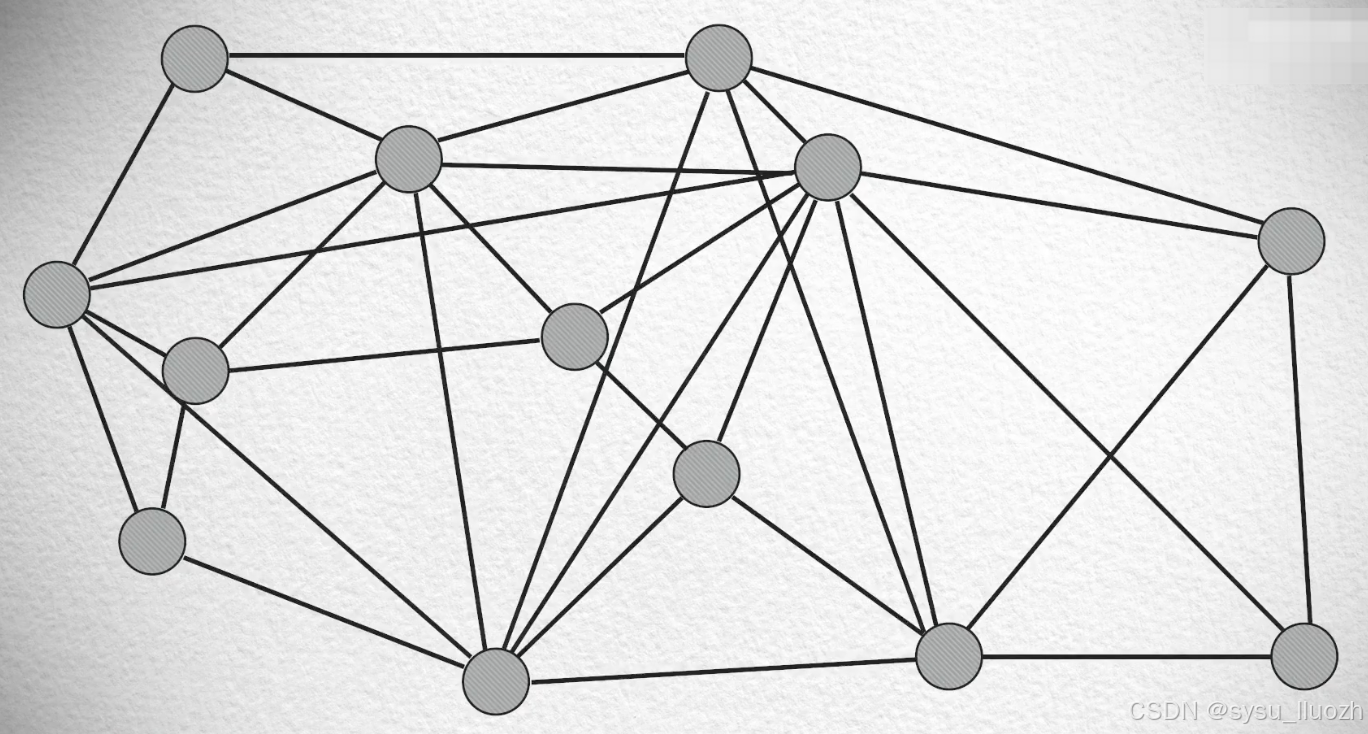
如果不看其中一些比较长的连接
发现这些"短线"形成的图近似于德劳内三角剖分法（Delaunay triangulation algorithm）建的图，拥有那三个美好性质。
在这里插入图片描述
如果只观察这些长的连接
则会发现另一个很好的性质，它们在搜索的过程中可以快速导航到目标节点

再配合短连接的细粒度的导航完成搜索

换句话说就是：先粗快，后细慢

而之所以会形成这些长的连接，是因为在随机逐个放回向量的初始阶段，向量点非常的稀疏，很容易在距离较远的点之间建立连接。

通过长连接快速导航，再通过短连接精细化搜索，这就是NSW算法大致的工作原理。

在NSW的基础上，后来又提出了它的"升级版"HNSW：分层导航小世界 - (Hierarchical) Navigable Small World

Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World graphs
使用分层导航小世界的高效且健壮的近似最近邻搜索

HNSW主要的思想并不复杂，就是在NSW的基础上向上添加了多个层级结构
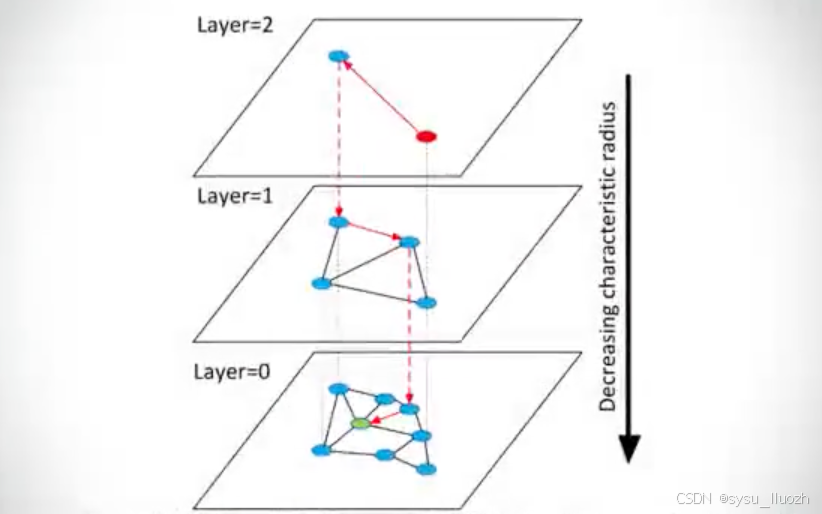
在这里插入图片描述
最下面一层包含全部节点的图结构，越往上层包含的节点数越少，最上面的节点最稀疏，但连线也最长，这有利于快速导航，而越下层的连接越短，这便于精细化的搜索。

如此在搜索的时候，从最上层开始，搜索的粒度很粗，但这保证了快速导航的发生。而后逐步进入下一层进行搜索，导航的速度越来越慢，但搜索的也越来越细。如此便同时实现了速度和效果的兼顾。
在这里插入图片描述

在NSW的长连接身上，已经发现了这个算法的核心奥义，那就是先粗后细。而HNSW相比于NSW最大的优势正是在于：这个由粗到细的过程更加可控和稳定。

在NSW中，搜索过程虽然大体上可能会利用长连接快速导航，然后再利用短连接精细查找。但是这是一个比较理想的情况，实际上搜索过程有一定的随机性，实际情况往往是随着数据量的增长，性能开始出现明显的疲软。但HNSW却能很大程度上改善这一点，因为在构建多层结构的时候就是按照自顶向下连接（平均）的长度逐渐变短来设计的。所以从顶部作为入口便就能保证先粗快后细慢的过程平稳的发生。

实际上HNSW的确是一个在速度和搜索效果上都非常出色的近似最近邻算法，但它也有一饿过相比于其他算法最为突出的缺点那就是：占用的内存空间极大。

以上就是本篇文章【【向量数据库】向量存储内存】的全部内容了，欢迎阅览！文章地址：http://w.yusign.com/quote/12008.html
行业资讯企业新闻行情企业黄页同类资讯网站地图返回首页述古往 http://w.yusign.com/mobile/ , 查看更多